– Ты можешь уподобить человеческую природу в отношении просвещенности и непросвещенности вот какому состоянию... Представь, что люди находятся в подземном жилище наподобие пещеры, где во всю ее длину тянется широкий просвет. С малых лет у них на ногах и на шее оковы, так что людям не двинуться с места, и видят они только то, что у них перед глазами, ибо повернуть голову они не могут из-за этих оков. Люди обращены спиной к свету, исходящему от огня, который далеко в вышине, а между светом и узниками проходит верхняя дорога, огражденная, представь, невысокой стеной, вроде той ширмы, за которой фокусники помещают своих помощников, когда поверх ширмы показывают кукол.
...
– За этой стеной другие люди несут различную утварь, держа ее так, что она видна поверх стены; проносят они и статуи и всяческие изображения живых существ, сделанные из камня и дерева.
...
– Разве ты думаешь, что находясь в таком положении, люди что-нибудь видят, свое или чужое, кроме теней, отбрасываемых огнем на расположенную перед ними стену пещеры?
– Как же им видеть что-то иное, раз всю свою жизнь они вынуждены держать голову неподвижно?
...
– Такие узники целиком и полностью принимали бы за истину тени проносимых мимо предметов.
«Государство».Платон
В эзотерических доктринах установлена следующая цепочка развития жизни и сознания: камень->растение->животное->человек. Возьмём эту цепочку за разумную основу в дальнейших рассуждениях, вспомним, что всё, что нас окружает, устроено по «законам меры, числа и гармонии», и на этом покинем пределы эзотерики (дабы не унестись в эмпиреи) и обратимся к научным фактам и их осмыслению, ибо «..самые красивые и замечательные теории гибнут под давлением гнусных экспериментальных фактов». В нашем случае всё наоборот, но давайте по-порядку...
«Правильные кристаллы»
Ни у кого не вызывает сомнений наличие жизни в растениях, животных и человеке, хотя происхождение растений до сих пор не понятно, да и в их жизнедеятельности масса удивительных и пока необъяснимых загадок, о чём можно подробней ознакомится в статье «Растения – параллельный мир». Будем искать признаки жизни в камнях, а точнее в кристаллах, что почти одно и то же. Но что нам искать? Будем искать симметрии, о чём недвусмысленно говорит заголовок к статье!
О важности симметрий в современной научной картине мира стоит поговорить особо в отдельной статье, мы же ограничимся цитатой из Википедии:
Некоторые симметрии в современной физике считаются точными, другие — лишь приближёнными. Также важную роль играет концепция спонтанного нарушения симметрии.
Исторически использование симметрии в физике прослеживается с древности, но наиболее революционным для физики в целом, по-видимому, стало применение такого принципа симметрии, как принцип относительности (как у Галилея, так и у Пуанкаре — Лоренца — Эйнштейна), ставшего затем как бы образцом для введения и использования в теорфизике других принципов симметрии (первым из которых стал, по-видимому, принцип общей ковариантности, являющимся достаточно прямым расширением принципа относительности и приведшего к общей теории относительности Эйнштейна).
В 1918 году немецкий математик Нётер доказала теорему, согласно которой каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения. Наличие этой теоремы позволяет проводить анализ физической системы на основе имеющихся данных о симметрии, которой эта система обладает. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.
В 1912 г. немецкий физик-теоретик Макс Лауэ сделал смелое предположение: в качестве дифракционной решетки для рентгеновских лучей можно использовать кристалл. В том же 1912 г. предположение Лауэ экспериментально проверили два его студента — В.Фридрих и П.Книппинг. Они пропустили рентгеновские лучи через кристалл медного купороса и получили на фотопластинке набор равномерно расположенных светлых точек — дифракционную картину. Таким образом, строение кристаллов, стало объектом практического изучения. Возникла новая научная дисциплина — кристаллография. В 1914 г. Лауэ была присуждена Нобелевская премия по физике «за открытие дифракции рентгеновских лучей на кристаллах».

На основе дифракционных картин, снятых под различными углами и дополненных расчетом, удалось установить форму элементарных ячеек, которые заполняют пространство. Оказалось, что это вертикальные или наклонные бруски, у которых размеры ребер и углы наклона различны.
Для нескольких сотен тысяч соединений были определены формы элементарных ячеек, и во всех основаниях их многогранников располагались только упомянутые многоугольники. Не было ни одного случая, что бы оказались пяти- семи- или десятиугольники. Причина - такие ячейки не могут плотно заполнить пространство. Кристалл оказался объемной мозаикой. К плоским мозаикам мы ещё вернёмся в конце статьи, ибо они неразрывно связаны с искомыми симметриями.
Запрещённая симметрия или «Этого просто не может быть!»
Оказалось, что они разместились в вершинах икосаэдра — многогранника, собранного из 20 правильных треугольников. Шехтман знал, что невозможно заполнить пространство икосаэдрами так, чтобы они плотно примыкали друг к другу, обязательно возникнут пустоты, чего в кристаллических телах не бывает.
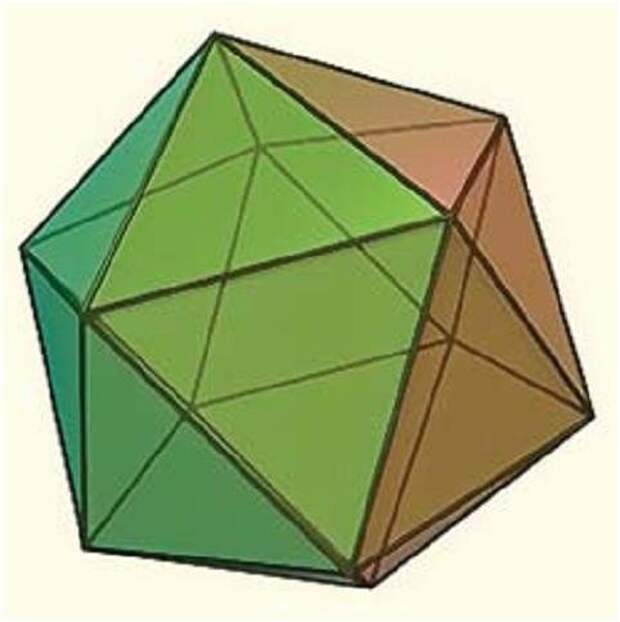 Удивление Шехтмана только усилилось. Итак, Шехтман получил отчетливую дифракционную картину из ярких точек. Если бы материал был не кристаллическим, а аморфным (например, как стекло), то вместо четких точек на экране было бы размытое беловатое пятно. Набор фиксированных точек означает, что имеется кристалл, следовательно, присутствует внутренний порядок. Но из икосаэдров невозможно построить периодически повторяющийся фрагмент, заполняющий пространство. Следовательно, возможен непериодический кристалл!— именно такой вывод сделал Шехтман.
Удивление Шехтмана только усилилось. Итак, Шехтман получил отчетливую дифракционную картину из ярких точек. Если бы материал был не кристаллическим, а аморфным (например, как стекло), то вместо четких точек на экране было бы размытое беловатое пятно. Набор фиксированных точек означает, что имеется кристалл, следовательно, присутствует внутренний порядок. Но из икосаэдров невозможно построить периодически повторяющийся фрагмент, заполняющий пространство. Следовательно, возможен непериодический кристалл!— именно такой вывод сделал Шехтман.Многие ведущие ученые не приняли выводы Шехтмана, хотя все желающие лаборатории повторили его опыты и подтвердили результаты. Что было самым драматическим для Даниэля — это враждебное отношение выдающегося химика ХХ в. Лайнуса Полинга, дважды лауреата Нобелевской премии, считавшегося непререкаемым авторитетом в химии. На одной из конференций Американского химического общества (Полинг был его президентом), собравшей больше тысячи химиков, он сообщил: «Дэн Шехтман говорит ерунду. Не существует такого понятия, как квазикристаллы, есть только квазиученые». Но, в конце концов, в 2011 году Шехтману была присуждена Нобелевская премия по химии за открытие квазикристаллов.
Рис. 5. Отдельные квазикристалы из различных сплавов
А что общего между кристаллами, нарушающими «разрешённые симметрии» и темой «Что такое Жизнь», спросите вы? А дело в том, что запрещённые в кристаллографии симметрии 5-го, 7-го и других порядков являются самыми распространёнными в живой природе. Можно сказать, что существует переходное звено между камнем и растением, обладающее общей симметрией.


Рис. 7.
Мозаика Жизни
В 1961 г. математик Хао Ванг высказал следующую гипотезу: любая мозаика из повторяющихся элементов всегда периодична. Но в 1966 г. его ученик, Роберт Бергер, доказал, что гипотеза Ванга неверна: Бергер создал непериодическую мозаику из 20 426 плиток, полностью замостив плоскость. Через некоторое время он, впрочем, сумел сократить их число до 104. Математики стали искать варианты мозаик, которые можно построить из меньшего количества плиток. В 1971 г. Рафаэль Робинсон предложил всего шесть плиток для непериодического замощения плоскости. К поиску в этом направлении подключился известный английский математик Роджер Пенроуз.
Пенроуз также сумел доказать, что при использовании более двух типов ромбовидных «кафельных плиток» можно создавать непериодические мозаики с участием семи- или 11-лучевых звезд. Он детально описал принципы создания таких мозаик и отметил, что эта область содержит много трудных и нерешенных пока задач.
Рис.9. Мозаики Пенроуза, собранные из плиток трех типов (слева) и из пяти. Каждый тип плитки имеет свою окраску
Долгое время считалось, что квазикристаллы можно создать только искусственным путем. Но в 2009 г. ученые из Принстонского университета обнаружили их во фрагментах минерала хатыркита (еще в 1979 г. он был найден российским геологом Валерием Крячко на Корякском нагорье). Это открытие так же вызвало небольшую сенсацию.

Рис.10. Образец минерала хатыркита (слева), элетронномикроскопический снимок природного квазикристалла (в середине), содержащегося в этом минерале, и фрагмент мозаики Пенроуза, которая удивительно напоминает полученный снимок.
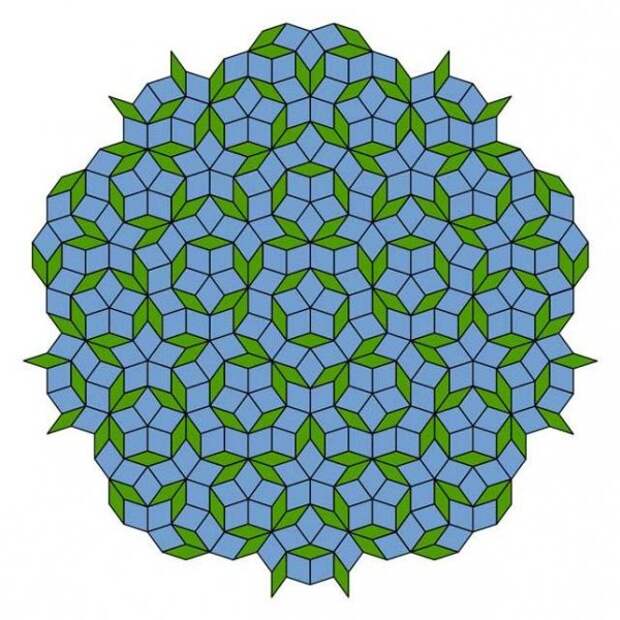
Примечательно, что возникший интерес к квазикристаллам вызвал новую волну в исследованиях историков и искусствоведов, изучающих древние орнаменты. Оказалось, что непериодические мозаики были известны по крайней мере за сотни лет до Пенроуза, а помогли в этом разобраться, естественно, математики. Они посмотрели свежим взглядом на узоры, покрывающие мечети в странах Азии (Афганистане, Иране, Ираке и Турции), построенные еще в Средневековье. Среди них, как оказалось, присутствовали пятиугольники и десятиугольники. Это первый признак того, что мозаика непериодическая, тщательный анализ подтвердил такие предположения.
Рис.11. Древний орнамент, украшающий свод у входа в султанскую ложу в турецкой мечети. 1424 г (слева). Непериодическая мозаика над входом в мечеть Дарб-и-Мам в Исфахане. 1453 г. (справа)
Появление подобных узоров относят к XIII в., а в XV в. они широко распространились. Большинство специалистов полагает, что столь сложные орнаменты не могли возникнуть случайно в процессе работы мастера при отделке зданий. Из результатов анализа, проведенного современными исследователями, стало ясно, что в орнаментах были соблюдены те же принципы, которые столетия спустя сформулировал Пенроуз. По-видимому, уровень развития средневековой математики на востоке был значительно выше, чем считалось до сих пор, ведь придумать такой орнамент без специальных математических знаний практически невозможно.
Интересно, что изменилась и терминология: под влиянием открытия Шехтмана все древние непериодические мозаики стали называть квазикристаллическими.
Вместо заключения
Хоть мы и занимались лишь тем, что разглядывали различные колеблющиеся тени, рисуемые нашим восприятием, но нам всё же удалось выявить весьма интересные взаимосвязи между совершенно различными явлениями нашего мира. В качестве отдыха предлагаю уважаемому читателю насладиться по-новому взглянуть на следующий короткий видеоролик:




Свежие комментарии