Возьмите простое решетчатое пространство. Задайте набор нехитрых правил. Запустите время. Вы получили клеточный автомат — почти что целый мир.
Правила «Жизни»
«Жизнь» существует на бесконечной решетчатой плоскости. Каждая клетка, имеющая двух или трех живых соседей, выживает на следующем шаге времени.
Если их меньше или больше, клетка умирает от «одиночества» или от «перенаселения». Если у мертвой клетки три живых соседа, она становится живой. Учитывается соседство по вертикали, горизонтали и диагонали. Вот и всё: базовые принципы игры исключительно просты, но могут порождать удивительно сложное поведение и разнообразие форм.

Правила «Жизни» были опубликованы кембриджским математиком Джоном Конвеем в 1970 году и сразу сделали клеточные автоматы невероятно популярными. Тысячи энтузиастов, ощутив себя в роли властелинов этого клетчатого мирка, принялись исследовать двумерные формы, которые рождаются и умирают в нем. Среди них обнаружились стационарные «натюрморты», способные существовать вечно без каких-либо изменений; периодические «осцилляторы», повторяющие одни и те же фигуры с определенной цикличностью; движущиеся «планеры», которые с каждым ходом смещаются в том или ином направлении.

Планер (глайдер) — перемещающаяся конфигурация из пяти клеток
Сегодня в «Жизни» известны миллионы таких существ: с ростом «размеров», то есть числа ячеек, количество возможных «натюрмортов» и «осцилляторов» увеличивается стремительно. Но уже в первые годы повального увлечения этим изящным клеточным автоматом выяснилось, что при наличии достаточного «жизненного» пространства в нем могут существовать и намного более сложные структуры. Например, «крепкий орешек» состоит из семи живых клеток, которые мучительно выживают на протяжении 130 поколений, после чего все разом аннигилируют.
Автомат становится машиной
Сам Конвей предполагал, что такая смертная судьба ждет любую нестационарную и непериодическую форму «Жизни», и даже объявил символическую премию тому, кто сможет доказать или опровергнуть идею о том, что на этом клетчатом поле возможно бесконечное размножение. Однако с обещанной суммой в $50 ему пришлось расстаться довольно быстро. В том же 1970 году Билл Госпер обнаружил периодическую структуру — «ружье», которое каждые 30 шагов возвращается к исходной конфигурации, рождая улетающий в сторону «планер». А вот это уже очень и очень любопытно...
Подобные «планерные ружья» можно рассматривать как генераторы импульсов, которыми обмениваются логические элементы любой вычислительной машины: ушел планер — единица, планера нет — ноль. Если пара таких планеров столкнется под прямым углом, то один из них аннигилирует, что позволяет моделировать логический элемент НЕ. Более сложными способами можно создать и другие элементы, выполняющие все базовые логические операции, включая И и ИЛИ. Остается их скомбинировать — и игра станет вычислительным устройством.

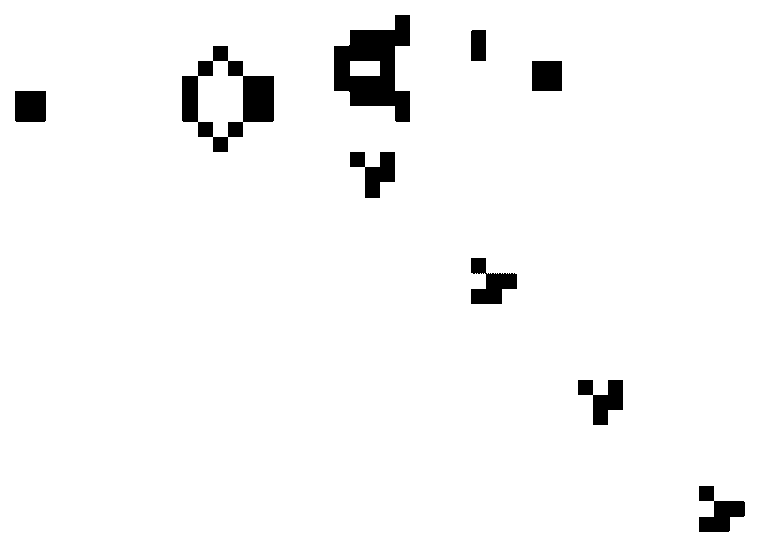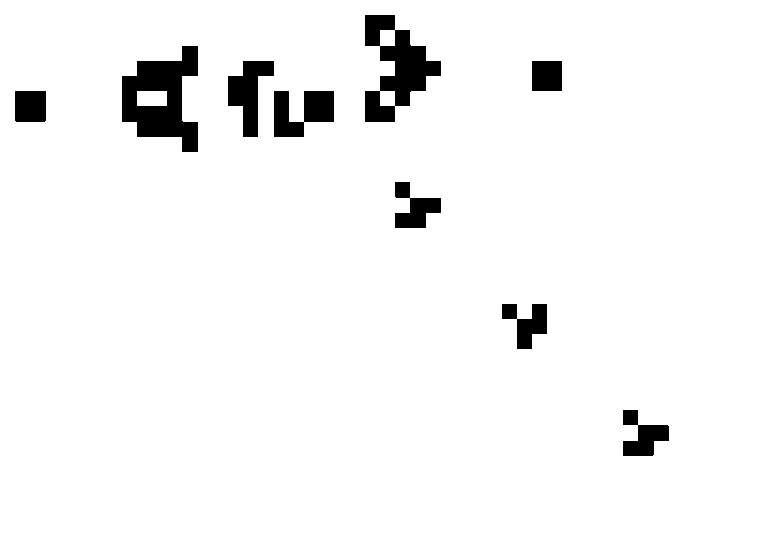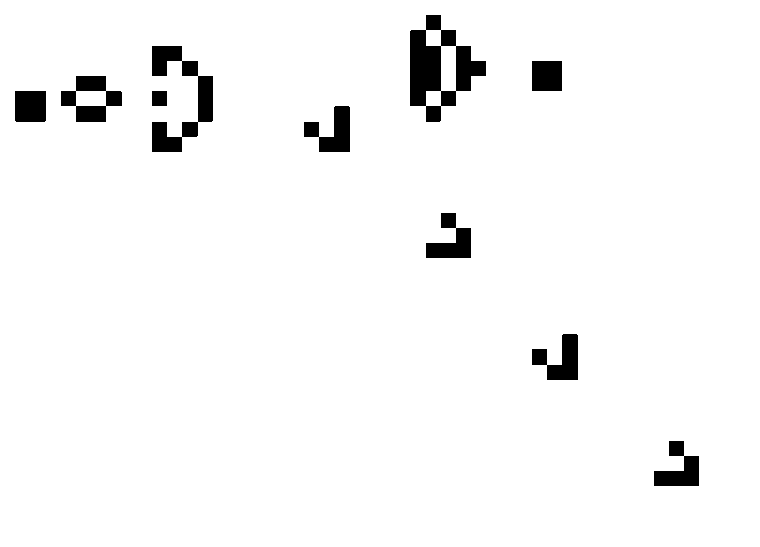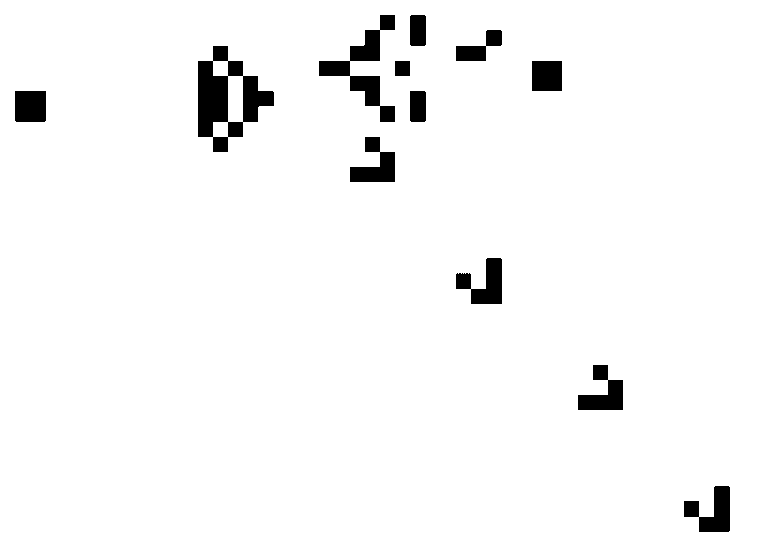
Впрочем, тот факт, что некоторые клеточные автоматы способны выполнять любые математические операции, эмулируя универсальную машину Тьюринга, был известен и до Конвея: в 1950-х этим воспользовался великий Джон фон Нейман. На волне всеобщей любви к робототехнике ученый задался вопросом, возможно ли сконструировать робота, который мог бы бесконечно самовоспроизводиться, штампуя собственные копии, чтобы они, в свою очередь, без конца производили новые поколения роботов.
Бесконечное рождение
Проектировать такой аппарат из металлической плоти и электрической крови было бы делом явно неблагодарным. Но вопрос достаточно было решить на принципиальном, математическом уровне, так же, как несколькими десятилетиями до того поступил с вычислительной машиной тот же Тьюринг. Идею фон Нейману подкинул коллега по Лос-Аламосской национальной лаборатории Станислав Улам, который использовал клеточные автоматы для исследований роста кристаллических структур.
Фон Нейман подобрал такое пространство бесконечной «шахматной доски», которое способно имитировать машину Тьюринга, и описал для нее конфигурацию примерно из 200 000 клеток, способную самовоспроизводиться бесконечной чередой поколений. Законы, управляющие эволюцией такого клеточного автомата, намного сложнее, чем у «Жизни», — достаточно упомянуть, что ячейки его могут принимать 29 различных значений, и для каждого перехода между ними требуется отдельное правило. Зато соседями — окрестностью каждой ячейки — в автомате фон Неймана считаются лишь те четыре, что расположены по вертикали и горизонтали от нее, тогда как у Конвея учитываются целых восемь ячеек, в том числе и находящиеся по диагонали от исходной (окрестность Мура).

Локальная зависимость поведения ячеек — такое же базовое свойство клеточных автоматов, как и глобальность правил, которые действуют совершенно одинаково в любой точке сетки. Это напоминает реальный мир: насколько нам известно, законы физики одинаковы в любой его точке, а вот взаимодействия распространяются с конечной скоростью, максимально — световой. В мире клеточных автоматов этот предел скорости еще заметнее. Любые изменения в «Жизни» в принципе не могут происходить быстрее скорости шахматного короля — на одну клетку за один интервал времени. Вообще, несмотря на кажущуюся простоту клеточных автоматов, процессы, которые происходят в них, в своей математической основе часто оказываются аналогичны реальным.
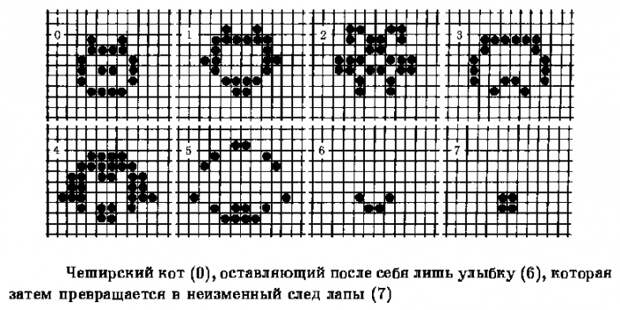
Хищники и жертвы
Возьмите стакан воды и вылейте ее на стол. Лучший из доступных способов предсказать ее движение — использовать суперкомпьютер, хотя и он способен дать лишь приблизительное решение запутанных уравнений гидродинамики. Но тот же процесс можно представить и в виде упрощенной модели «решеточного газа», ячейки которого могут содержать или не содержать молекул. Это позволит описать их поведение с помощью набора кратких правил. Например: течение увлекает молекулу вниз, пока она не встретит препятствие — стол или другую молекулу — в этом случае она перемещается в случайную незанятую ячейку сбоку. Мы получим нехитрый клеточный автомат, который способен с приемлемой точностью имитировать реальность.
Схожие правила позволяют моделировать поведение толпы. Если есть возможность, человек движется вперед; встретив препятствие, повернет в сторону; если по сторонам стоят другие люди, останется на месте. Окрестность в этом случае придется учитывать более дальнюю, введя вероятность перемещения в том или ином направлении в зависимости от присутствия других людей или стен — «глядя» на несколько клеток вперед. Варьируя эти параметры, можно с точностью моделировать движение людского потока и использовать эти результаты при проектировании городского пространства.
Существуют клеточные автоматы, которые моделируют колебательные химические реакции и работу дыхательных устьиц растительного листа, турбулентные процессы и образование узора на раковинах моллюсков, динамику численности популяций травоядных и хищников. Правила просты. Особь может переместиться на случайную из клеток в окрестности Неймана. С определенной периодичностью она оставляет в исходной клетке потомка, с определенной — сама умирает от старости. Хищная особь может проглотить соседнее травоядное, а если не сделает этого в течение некоторого времени, то погибнет от голода. Такой клеточный автомат позволяет получить характерные S-образные кривые популяционного роста: численность хищников и травоядных выйдет на определенный уровень и будет колебаться около него. Всё как в жизни.

Клетчатый мир
Схожесть жизни с клеточными автоматами давно интригует ученых. Эти идеи максимально развиты у Конрада Цузе, а позднее — у Эдварда Фредкина, сформулировавшего свою «конечную гипотезу»: «Всякая физическая величина, включая время и пространство, является конечной и дискретной». Квантуемость пространства-времени остается недоказанной, однако на эти представления опираются некоторые вполне уважаемые теории, включая петлевую квантовую гравитацию.
Отсюда остается сделать последний шаг. Если Вселенную представить как дискретное поле, ячейки которого меняются в соответствии с определенными законами, то не является ли она по сути клеточным автоматом? Работа его создает иллюзию существования частиц, полей и взаимодействий, которые на самом деле — лишь разные состояния очень маленьких «элементарных ячеек» мироздания, изменяющихся за чрезвычайно краткие промежутки времени.
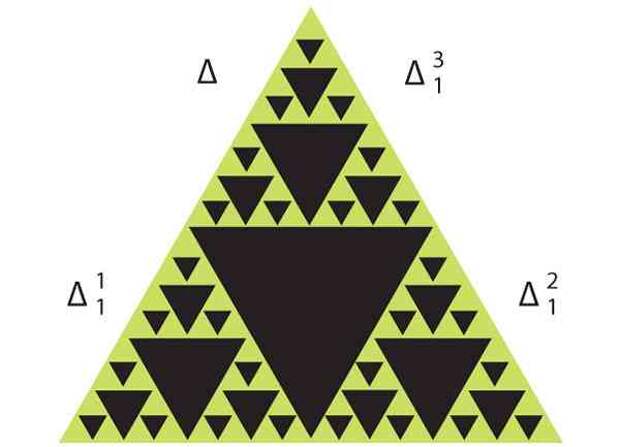
Эволюцию одномерного клеточного автомата можно представить на плоскости, одним из измерений которой будет время. Один из таких автоматов создает фрактальную структуру «салфетки Серпинского»
Матрица «шахматной доски» Конвея превращается в глобальную матрицу нашего мира — динамичную и завораживающую. Впрочем, взгляды «цифровой физики», главным апологетом которой сегодня выступает Стивен Вольфрам, нельзя назвать общепринятыми среди ученых. «Монитор вашего компьютера, изображение на котором состоит из точек-пикселей, доказывает, что такой мир может выглядеть вполне реалистично, — пишет нобелевский лауреат Фрэнк Вильчек. — Но в нем обязательно что-то будет немного не так».
P.S.
Предложенный Конвеем свод правил, или ЗАКОН, — лишь один из многих возможных. При данных начальных условиях существует "два в степени два в степени девять" т.е. около 10154 различных "жизнеподобных" законов, из которых, похоже, только ОДИН, установленный Конвеем, оказался жизнеспособен.
М. Шредер "Фракталы, хаос, степенные законы"
P.P.S.
Очень простые правила образуют очень сложные структуры, примеры которых в динамике на видео. Может кому-то что-то они напоминают?
Свежие комментарии