
В стародавние времена люди думали» что 3емля плоская и стоит на трех китах, затем выяснилось, что наша ойкумена круглая и, если плыть все время на запад, то через некоторое время вернешься в исходную точку с востока. Похожим образом изменялись и воззрения на Вселенную. В свое время Ньютон полагал, что пространство плоское и бесконечное. Эйнштейн разрешил нашему Миру быть не только безграничным и кривым, но и замкнутым. Новейшие данные, полученные в процессе исследования реликтового излучения, свидетельствуют о том, что Вселенная вполне может быть замкнута сама на себя. Получается, что если все время лететь от 3емли, то в какой-то момент начнешь к ней приближаться и в конце концов вернешься назад, обойдя всю Вселенную и совершив кругосветное путешествие, подобно тому, как один из кораблей Магеллана, обогнув весь земной шар, приплыл в испанский порт Санлукар-де-Баррамеда.
Гипотеза о том, что наша Вселенная родилась в результате Большого взрыва, сейчас считается общепринятой. Материя вначале была очень горячей, плотной и быстро расширялась. Затем температура Вселенной понизилась до нескольких тысяч градусов. Вещество в этот момент состояло из электронов, протонов и альфа-частиц (ядер гелия), то есть представляло собой сильно ионизированный газ — плазму, непрозрачную для света и любых электромагнитных волн. Начавшаяся в это время рекомбинация (соединение) ядер и электронов, то есть образование нейтральных атомов водорода и гелия, кардинально изменила оптические свойства Вселенной. Она стала прозрачной для большинства электромагнитных волн.
Таким образом, изучая свет и радиоволны, можно увидеть только то, что произошло после рекомбинации, а все то, что случилось раньше, закрыто он нас своеобразной «огненной стеной» ионизованного вещества. Заглянуть гораздо глубже в историю Вселенной можно только в том случае, если мы научимся регистрировать реликтовые нейтрино, для которых горячее вещество стало прозрачным гораздо раньше, и первичные гравитационные волны, для которых материя любой плотности — не преграда, однако это дело будущего, причем далеко не самого близкого.
С момента образования нейтральных атомов наша Вселенная расширилась примерно в 1 000 раз, и излучение эпохи рекомбинации сегодня наблюдается на Земле как реликтовый микроволновый фон с температурой около трех градусов Кельвина. Этот фон, впервые обнаруженный в 1965 году при испытаниях большой радиоантенны, практически одинаков во всех направлениях. По современным данным, реликтовых фотонов в сто миллионов раз больше, чем атомов, поэтому наш мир просто купается в потоках сильно покрасневшего света, излученного еще в самые первые минуты жизни Вселенной.
Классическая топология пространства
На масштабах больших, чем 100 мегапарсек, видимая нами часть Вселенной достаточно однородна. Все плотные сгустки материи — галактики, их скопления и сверхскопления — наблюдаются только на меньших расстояниях. Более того, Вселенная к тому же изотропна, то есть ее свойства одинаковы вдоль любого направления. Эти экспериментальные факты лежат в основе всех классических космологических моделей, в которых предполагаются сферическая симметрия и пространственная однородность распределения вещества.
Классические космологические решения уравнений общей теории относительности Эйнштейна (ОТО), которые были найдены в 1922 году Александром Фридманом, имеют простейшую топологию. Их пространственные сечения напоминают плоскости (для бесконечных решений) или сферы (для ограниченных решений). Но у подобных вселенных, оказывается, существует альтернатива: не имеющая краев и границ, замкнутая сама на себя вселенная конечного объема.
Первые решения, найденные Фридманом, описывали вселенные, заполненные только одним сортом вещества. Различные картины возникали из-за разницы в средней плотности материи: если она превышала критический уровень, получалась замкнутая вселенная с положительной пространственной кривизной, конечными размерами и временем жизни. Ее расширение постепенно замедлялось, останавливалось и сменялось сжатием в точку. Вселенная с плотностью ниже критической имела отрицательную кривизну и бесконечно расширялась, скорость ее раздувания стремилась к некоторой постоянной величине. Эта модель называется открытой. Плоская Вселенная — промежуточный случай с плотностью, точно равной критической, — бесконечна и ее мгновенные пространственные сечения являются плоским евклидовым пространством с нулевой кривизной. Плоская, так же как и открытая, расширяется бесконечно долго, но скорость ее расширения при этом стремится к нулю. Позднее были придуманы более сложные модели, в которых однородная и изотропная вселенная была заполнена многокомпонентным веществом, видоизменяющимся со временем.
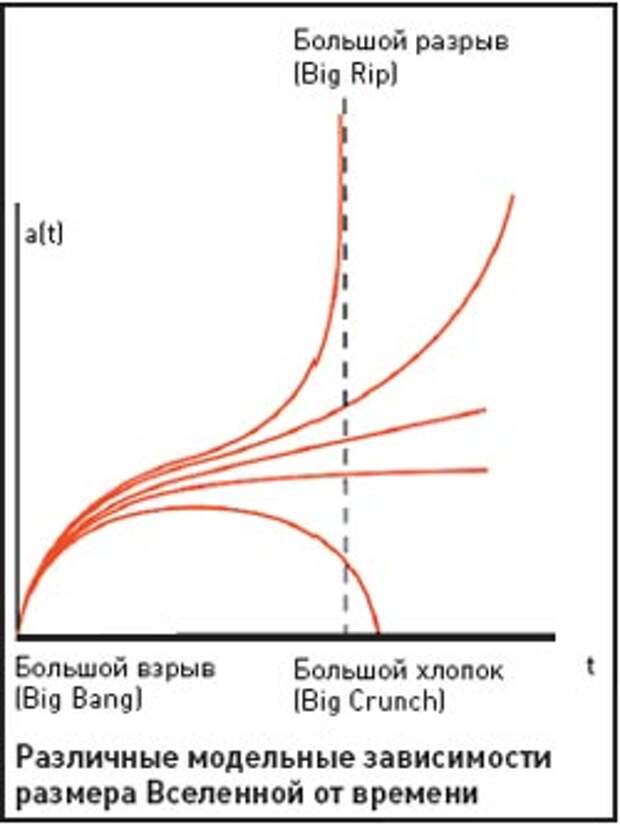 Современные наблюдения показывают, что сейчас Вселенная расширяется с ускорением (см. «За горизонтом вселенских событий», № 3, 2006). Такое поведение возможно, если пространство заполнено неким веществом (называемым часто темной энергией) с высоким отрицательным давлением, близким к плотности энергии этого вещества. Это свойство темной энергии приводит к возникновению как бы антигравитации, которая преодолевает на больших масштабах силы притяжения обычной материи. Первая подобная модель (с так называемым лямбдачленом) была предложена еще самим Альбертом Эйнштейном.
Современные наблюдения показывают, что сейчас Вселенная расширяется с ускорением (см. «За горизонтом вселенских событий», № 3, 2006). Такое поведение возможно, если пространство заполнено неким веществом (называемым часто темной энергией) с высоким отрицательным давлением, близким к плотности энергии этого вещества. Это свойство темной энергии приводит к возникновению как бы антигравитации, которая преодолевает на больших масштабах силы притяжения обычной материи. Первая подобная модель (с так называемым лямбдачленом) была предложена еще самим Альбертом Эйнштейном.
Особый режим расширения Вселенной возникает, если давление этой материи не остается постоянным, а возрастает со временем. В этом случае увеличение размеров нарастает настолько быстро, что Вселенная становится бесконечной за конечное время. Такое резкое раздувание пространственных размеров, сопровождаемое разрушением всех материальных объектов, от галактик до элементарных частиц, получило название Большого разрыва (Big Rip).
Все эти модели не предполагают каких-либо особых топологических свойств у Вселенной и представляют ее похожей на наше привычное пространство. Такая картина хорошо согласуется с теми данными, которые астрономы получают с помощью телескопов, регистрирующих инфракрасное, видимое, ультрафиолетовое и рентгеновское излучения. И только данные радионаблюдений, а именно детальное изучение реликтового фона, заставили ученых усомниться в том, что наш мир устроен столь прямолинейно.
Заглянуть за «огненную стену», отделяющую нас от событий первых тысяч лет жизни нашей Вселенной, ученым удастся не скоро. Зато с помощью выводимых в космос лабораторий мы с каждым годом все больше узнаем о том, что происходило после превращения горячей плазмы в теплый газ
Орбитальный радиоприемник
Первые результаты, полученные космической обсерваторией WMAP (Wilkinson Microwave Anisotropy Probe), измерявшей мощность реликтового излучения, были опубликованы в январе 2003 года и содержали так много долгожданной информации, что ее осознание не завершено и сегодня. Обычно для объяснения новых космологических данных используют физику: уравнения состояния вещества, законы расширения и спектры начальных возмущений. Но в этот раз характер обнаруженной угловой неоднородности излучения потребовал совсем другого объяснения — геометрического. Более же точно — топологического.
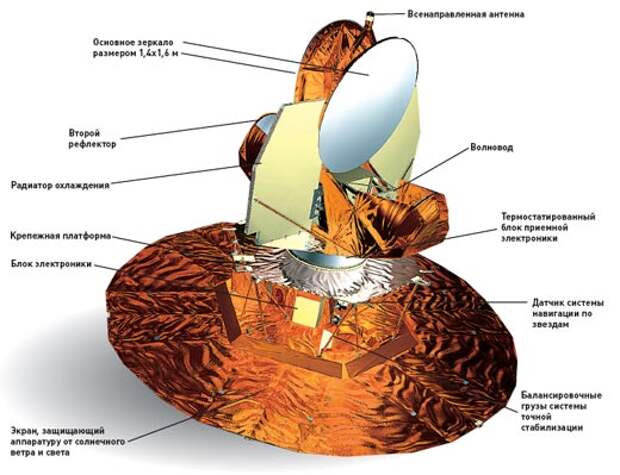
Основной целью WMAP было построение подробной карты температуры реликтового излучения (или, как его еще называют, микроволнового фона). WMAP — это сверхчувствительный радиоприемник, одновременно регистрирующий сигналы, приходящие из двух почти диаметрально противоположных точек неба. Обсерватория была запущена в июне 2001 года на особо спокойную и «тихую» орбиту, находящуюся в так называемой лагранжевой точке L2 в полутора миллионах километров от Земли. Этот спутник весом 840 кг на самом деле находится на околосолнечной орбите, однако благодаря совместному действию гравитационных полей Земли и Солнца период его обращения в точности равен одному году, и он никуда не улетает от Земли. На такую далекую орбиту спутник был запущен для того, чтобы помехи от земной техногенной активности не мешали приему реликтового радиоизлучения.
На основе полученных космической радиообсерваторией данных удалось с беспрецедентной точностью определить огромное количество космологических параметров. Во-первых, отношение полной плотности Вселенной к критической — 1,02±0,02 (то есть наша Вселенная плоская или замкнутая с очень малой кривизной). Во-вторых, постоянную Хаббла, характеризующую расширение нашего Мира на больших масштабах, — 72±2 км/с/Мпк. В-третьих, возраст Вселенной — 13,4±0,3 млрд. лет и красное смещение, соответствующее времени рекомбинации, — 1088±2 (это среднее значение, толщина границы рекомбинации существенно больше указанной ошибки). Наиболее сенсационным для теоретиков результатом стал угловой спектр возмущений реликтового излучения, точнее, слишком маленькая величина второй и третьей гармоники.
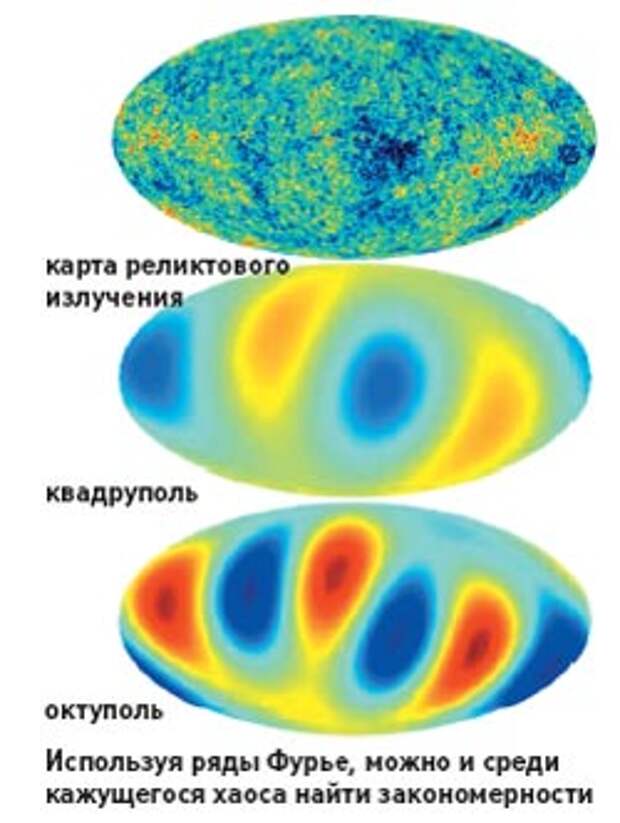
Такой спектр строится путем представления температурной карты в виде суммы различных сферических гармоник (мультиполей). При этом из общей картины возмущений выделяются переменные составляющие, укладывающиеся на сфере целое число раз: квадруполь — 2 раза, октуполь — 3 раза, и так далее. Чем выше номер сферической гармоники, тем более высокочастотные колебания фона она описывает и тем меньше угловой размер соответствующих «пятен». Теоретически число сферических гармоник бесконечно, но для реальной карты наблюдений оно ограничивается тем угловым разрешением, с которым проводились наблюдения.
Для корректного измерения всех сферических гармоник необходима карта всей небесной сферы, и WMAP получает ее верифицированный вариант как раз за год. Первые такие не очень подробные карты были получены в 1992 году в экспериментах «Реликт» и COBE (Cosmic Background Explorer).
 Чем бублик похож на кофейную чашку
Чем бублик похож на кофейную чашку
Есть такой раздел математики — топология, которая исследует свойства тел, сохраняющиеся при любых их деформациях без разрывов и склеек. Представьте себе, что интересующее нас геометрическое тело гибкое и легко деформируется. В этом случае, например, куб или пирамиду можно легко преобразовать в сферу или бутылку, тор («бублик») — в кофейную чашку с ручкой, а вот превратить сферу в чашку с ручкой не удастся, если не разрывать и не склеивать данное легко деформируемое тело. Для того чтобы разделить сферу на два несвязанных кусочка, достаточно провести один замкнутый разрез, а сделать то же самое с тором можно, лишь произведя два разреза. Топологи просто обожают всякого рода экзотические конструкции типа плоского тора, рогатой сферы или бутылки Клейна, которые можно корректно изобразить только в пространстве с вдвое большим числом измерений. Так и нашу трехмерную Вселенную, замкнутую саму на себя, можно себе легко представить, только живя в шестимерном пространстве. На время космические топологи пока не покушаются, оставляя ему возможность просто линейно течь, ни на что не замыкаясь. Так что умения работать в пространстве семи измерений сегодня вполне достаточно для понимания того, как сложно устроена наша додекаэдрическая Вселенная.
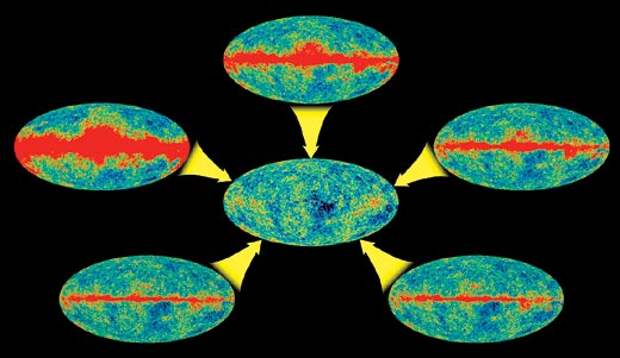
Итоговая карта температуры реликтового излучения строится на основе кропотливого анализа карт, отображающих интенсивность радиоизлучения в пяти различных частотных диапазонах
Неожиданное решение
Для большинства сферических гармоник полученные экспериментальные данные совпали с модельными расчетами. Только две гармоники, квадруполь и октуполь, оказались явно ниже ожидаемого теоретиками уровня. Причем вероятность того, что столь большие отклонения могли возникнуть случайно, крайне мала. Подавление квадруполя и октуполя было отмечено еще в данных COBE. Однако карты, полученные в те годы, имели плохое разрешение и большие шумы, поэтому обсуждение этого вопроса было отложено до лучших времен. По какой причине амплитуды двух самых крупномасштабных флуктуаций интенсивности реликтового излучения оказались столь маленькими, вначале было совершенно непонятно. Придумать физический механизм для их подавления пока не удалось, поскольку он должен действовать на масштабе всей наблюдаемой нами Вселенной, делая ее более однородной, и при этом переставать работать на меньших масштабах, позволяя ей флуктуировать сильнее. Наверное, поэтому начали искать альтернативные пути и нашли топологический ответ на возникший вопрос. Математическое решение физической проблемы оказалось удивительно изящным и неожиданным: достаточно было предположить, что Вселенная — замкнутый сам на себя додекаэдр. Тогда подавление низкочастотных гармоник можно объяснить пространственной высокочастотной модуляцией фонового излучения. Этот эффект возникает за счет многократного наблюдения одной и той же области рекомбинирующей плазмы через разные участки замкнутого додекаэдрического пространства. Получается, что низкие гармоники как бы гасят сами себя за счет прохождения радиосигнала через разные грани Вселенной. В такой топологической модели мира события, происходящие вблизи одной из граней додекаэдра, оказываются рядом и с противоположной гранью, поскольку эти области тождественны и на самом деле являются одной и той же частью Вселенной. Из-за этого реликтовый свет, приходящий на Землю с диаметрально противоположных сторон оказывается излученным одной и той же областью первичной плазмы. Это обстоятельство приводит к подавлению низших гармоник спектра реликтового излучения даже во Вселенной лишь немногим большей по размеру горизонта видимых событий.
 Карта анизотропии
Карта анизотропии
Упоминающийся в тексте статьи квадруполь не является самой низкой сферической гармоникой. Кроме него существуют монополь (нулевая гармоника) и диполь (первая гармоника). Величина монополя определяется средней температурой реликтового излучения, которая сегодня равняется 2,728 K. После его вычитания из общего фона самой большой оказывается дипольная компонента, показывающая, насколько температура в одной из полусфер окружающего нас пространства выше, чем в другой. Наличие этой компоненты вызвано в основном движением Земли и Млечного Пути относительно реликтового фона. Из-за эффекта Доплера температура в направлении движения повышается, а в противоположном — понижается. Данное обстоятельство позволит определить скорость любого объекта по отношению к реликтовому излучению и таким образом ввести долгожданную абсолютную систему координат, локально покоящуюся по отношению ко всей Вселенной.
Величина дипольной анизотропии, связанная с движением Земли, составляет 3,353*10-3 K. Это соответствует движению Солнца относительно фона реликтового излучения со скоростью около 400 км/с. «Летим» мы при этом в направлении границы созвездий Льва и Чаши, а «улетаем» из созвездия Водолея. Наша Галактика вместе с локальной группой галактик, куда она входит, движется относительно реликта со скоростью около 600 км/с.
Все остальные возмущения (начиная с квадруполя и выше) на карте фона вызваны неоднородностями плотности, температуры и скорости вещества на границе рекомбинации, а также радиоизлучением нашей Галактики. После вычитания дипольной компоненты суммарная амплитуда всех остальных отклонений оказывается всего 18*10-6 K. Для исключения собственного излучения Млечного Пути (в основном сосредоточенного в плоскости галактического экватора) наблюдения микроволнового фона ведутся в пяти частотных полосах в диапазоне от 22,8 ГГц до 93,5 ГГц.
 Комбинации с тором
Комбинации с тором
Простейшим телом с более сложной, чем сфера или плоскость, топологией является тор. Представить его может каждый, кто держал в руках бублик. Другую более корректную математическую модель плоского тора демонстрируют экраны некоторых компьютерных игр: это квадрат или прямоугольник, противоположные стороны которого отождествлены, и если движущийся предмет уходит вниз, то появляется сверху; пересекая левую границу экрана, он появляется из-за правой, и наоборот. Такой тор является простейшим примером мира с нетривиальной топологией, который имеет конечный объем и при этом не имеет каких-либо границ.
В трехмерном пространстве аналогичную процедуру можно проделать с кубом. Если отождествить его противоположные грани, то образуется трехмерный тор. Если посмотреть изнутри такого куба на окружающее пространство, то можно увидеть бесконечный мир, состоящий из копий его одной-единственной и уникальной (не повторяющейся) части, объем которой вполне конечен. В таком мире нет каких-либо границ, но есть три выделенных направления, параллельных ребрам исходного куба, вдоль которых наблюдаются периодические ряды исходных предметов. Эта картина очень похожа на то, что можно увидеть внутри кубика с зеркальными стенками. Правда, взглянув на любую из его граней, обитатель такого мира увидит свой затылок, а не лицо, как в земной комнате смеха. Более правильной моделью будет комната, оборудованная 6 телекамерами и 6 плоскими ЖК-мониторами, на которые выводится изображение, снимаемое расположенной напротив кинокамерой. В этой модели видимый мир замыкается сам на себя благодаря выходу в иное телевизионное измерение.
Описанная выше картина подавления низкочастотных гармоник верна, если время, за которое свет пересекает исходный объем, достаточно мало, то есть если размеры начального тела малы по сравнению с космологическими масштабами. Если же размеры доступной для наблюдений части Вселенной (так называемого горизонта Вселенной) оказываются меньше размеров исходного топологического объема, то ситуация не будет ничем отличаться от той, что мы увидим в обычной бесконечной эйнштейновской Вселенной, и никаких аномалий в спектре реликтового излучения наблюдаться не будет.
Максимально возможный пространственный масштаб в таком кубическом мире определяется размерами исходного тела — расстояние между любыми двумя телами не может превышать половины главной диагонали исходного куба. Свет, идущий к нам от границы рекомбинации, может по дороге несколько раз пересечь исходный куб, как бы отражаясь в его зеркальных стенках, из-за этого угловая структура излучения искажается и низкочастотные флуктуации становятся высокочастотными. В результате чем меньше исходный объем, тем сильнее подавление низших крупномасштабных угловых флуктуаций, а значит, изучая реликтовый фон, можно оценить размеры нашей Вселенной.
Трехмерные мозаики
Плоскую топологически сложную трехмерную Вселенную можно построить только на основе кубов, параллелепипедов и шестигранных призм. В случае искривленного пространства такими свойствами обладает более широкий класс фигур. При этом наиболее хорошо полученные в эксперименте WMAP угловые спектры согласуются с моделью Вселенной, имеющей форму додекаэдра. Этот правильный многогранник, имеющий 12 пятиугольных граней, напоминает футбольный мячик, сшитый из пятиугольных лоскутков. Оказывается, что в пространстве с небольшой положительной кривизной правильными додекаэдрами можно без дыр и взаимных пересечений заполнить все пространство. При определенном соотношении между размером додекаэдра и кривизной для этого надо 120 сферических додекаэдров. Более того, эту сложную структуру из сотни «мячиков» можно свести к топологически эквивалентной, состоящей всего из одного-единственного додекаэдра, у которого отождествлены повернутые на 180 градусов противоположные грани.
Вселенная, образованная из такого додекаэдра, обладает рядом интересных свойств: в ней нет выделенных направлений, и она лучше большинства других моделей описывает величину низших угловых гармоник реликтового фона. Такая картина возникает только в замкнутом мире с отношением действительной плотности вещества к критической 1,013, что попадает в интервал значений, допустимых сегодняшними наблюдениями (1,02±0,02).
Для рядового жителя Земли все эти топологические хитросплетения на первый взгляд не имеют особого значения. А вот для физиков и философов — совсем другое дело. Как для мировоззрения в целом, так и для единой теории, объясняющей строение нашего мира, эта гипотеза представляет большой интерес. Поэтому, обнаружив аномалии в спектре реликта, ученые стали искать другие факты, способные подтвердить или опровергнуть предложенную топологическую теорию.
 Звучащая плазма
Звучащая плазма
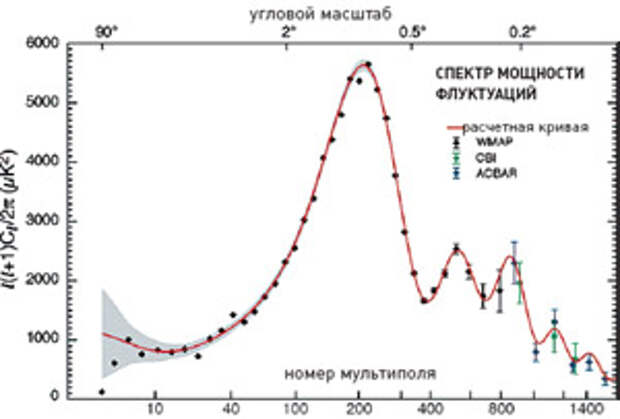
На спектре флуктуаций реликтового фона красной линией обозначены предсказания теоретической модели. Серый коридор вокруг нее — допустимые отклонения, а черные точки — результаты наблюдений. Большая часть данных получена в эксперименте WMAP, и только для самых высоких гармоник добавлены результаты исследований CBI (баллонные) и ACBAR (наземные антарктические). На нормированном графике углового спектра флуктуаций реликтового излучения видно несколько максимумов. Это так называемые «акустические пики», или «Сахаровские осцилляции». Их существование было теоретически предсказано Андреем Сахаровым. Эти пики обусловлены эффектом Доплера и вызваны движением плазмы в момент рекомбинации. Максимальная амплитуда колебаний приходится на размер причинно-связанной области (звукового горизонта) в момент рекомбинации. На меньших масштабах плазменные колебания были ослаблены фотонной вязкостью, а на больших — возмущения не зависели друг от друга и не были сфазированы. Поэтому максимум флуктуаций, наблюдаемых в современную эпоху, приходится на углы, под которыми сегодня виден звуковой горизонт, то есть область первичной плазмы, жившая единой жизнью в момент рекомбинации. Точное положение максимума зависит от отношения полной плотности Вселенной к критической. Наблюдения показывают, что первый, самый высокий пик расположен примерно на 200-й гармонике, что по теории с высокой точностью соответствует плоской Евклидовой Вселенной.
Очень много информации о космологических параметрах содержится во втором и последующих акустических пиках. Само их существование отражает факт «сфазированности» акустических колебаний в плазме в эпоху рекомбинации. Если бы такой связи не было, то наблюдался бы только первый пик, а флуктуации на всех меньших масштабах были бы равновероятными. Но для того чтобы подобная причинная связь колебаний в разных масштабах могла возникнуть, эти (очень сильно удаленные друг от друга) области должны были иметь возможность взаимодействовать друг с другом. Именно такая ситуация естественным образом возникает в модели инфляционной Вселенной, а уверенное обнаружение второго и следующих пиков в угловом спектре флуктуаций реликтового излучения является одним из наиболее весомых подтверждений этого сценария.
Наблюдения реликтового излучения велись в области, близкой к максимуму теплового спектра. Для температуры 3K он находится на длине волны радиоизлучения 1мм. WMAP вел свои наблюдения на чуть более длинных волнах: от 3 мм до 1,5 см. Этот диапазон достаточно близок к максимуму, и в нем ниже шумы от звезд нашей Галактики.
 Многогранный мир
Многогранный мир
В додекаэдральной модели горизонт событий и лежащая очень близко к нему граница рекомбинации пересекают каждую из 12 граней додекаэдра. Пересечение границы рекомбинации и исходного многогранника образуют на карте микроволнового фона 6 пар кругов, расположенных в противоположных точках небесной сферы. Угловой диаметр этих кругов — 70 градусов. Эти круги лежат на противоположных гранях исходного додекаэдра, то есть они геометрически и физически совпадают. Вследствие этого распределение флуктуаций реликтового излучения вдоль каждой пары кругов должно совпадать (с учетом поворота на 180 градусов). На основе имеющихся данных такие круги пока что не были обнаружены.
Но это явление, как оказалось, имеет более сложный характер. Круги будут одинаковыми и симметричными только для наблюдателя, неподвижного относительно реликтового фона. Земля же движется относительно него с достаточно высокой скоростью, из-за чего в фоновом излучении появляется существенная дипольная компонента. В этом случае круги превращаются в эллипсы, меняются их размеры, расположение на небе и среднее значение температуры вдоль круга. Обнаружить тождественные круги при наличии подобных искажений становится гораздо труднее, и точности имеющихся сегодня данных становится недостаточно — нужны новые наблюдения, которые помогут разобраться с тем, есть они или их все же нет.
Многосвязная инфляция
Пожалуй, самая серьезная проблема всех топологически сложных космологических моделей, а их возникло уже немалое количество, имеет в основном теоретический характер. Сегодня стандартным считается инфляционный сценарий эволюции Вселенной. Он был предложен для объяснения высокой однородности и изотропности наблюдаемой Вселенной. Согласно ему вначале родившаяся Вселенная была достаточно неоднородной. Затем в процессе инфляции, когда Вселенная расширялась по близкому к экспоненте закону, ее изначальные размеры возросли на много порядков. Сегодня мы видим только малую часть Большой Вселенной, в которой по-прежнему остались неоднородности. Правда, они имеют столь большую пространственную протяженность, что внутри доступной нам области незаметны. Инфляционный сценарий пока является лучше всего разработанной космологической теорией.
Для многосвязной вселенной такая последовательность событий не подходит. В ней доступна для наблюдения вся ее уникальная часть и некоторые из ее ближайших копий. В таком случае структуры или процессы, описываемые масштабами, много большими наблюдаемого горизонта, существовать не могут.
Направления, в которых придется развивать космологию, если многосвязность нашей Вселенной подтвердится, уже ясны: это безинфляционные модели и так называемые модели со слабой инфляцией, в которых размеры вселенной за время инфляции возрастают всего в несколько раз (или десятков раз). Таких моделей пока нет, и ученые, стараясь сохранить привычную картину мира, активно ищут огрехи в результатах, полученных с помощью космического радиотелескопа.
Артефакты обработки
Одна из групп, которая вела самостоятельные исследования данных WMAP, обратила внимание на то, что квадрупольная и октупольная составляющие реликтового излучения имеют близкую друг к другу ориентацию и лежат в плоскости, почти совпадающей с галактическим экватором. Вывод этой группы: произошла ошибка при вычитании фона Галактики из данных наблюдений микроволнового фона и реальная величина гармоник совсем другая.
Наблюдения WMAP велись на 5 различных частотах специально для того, чтобы правильно разделить космологический и локальный фон. И основная команда WMAP считает, что обработка наблюдений была проведена корректно, и отвергает предложенное объяснение.
Имеющиеся космологические данные, опубликованные еще в начале 2003 года, были получены после обработки результатов только первого года наблюдений WMAP. Для проверки предложенных гипотез, как обычно, требуется повышение точности. К началу 2006 года WMAP ведет непрерывные наблюдения уже четыре года, этого должно хватить для повышения точности вдвое, но эти данные все еще не опубликованы. Нужно немного подождать, и, возможно, наши предположения о додекаэдрической топологии Вселенной примут вполне доказательный характер.
Михаил Прохоров, доктор физико-математических наук
Может ли наша Вселенная быть конечной и топологически сложной?
В самом начале 2003 года появились первые данные наблюдений реликтового фона, выполненные на космическом зонде WMAP (Wilkinson Microwave Anisotropy Probe). Впервые множество космологических параметров были измерены с необычайно высокой точностью. Но за несколько месяцев первые, самые важные результаты и предсказания были сделаны, восторги поутихли и любопытство ученых переместилось от полученных результатов к проблемам, оставшимся необъясненными.
Наблюдения
Одна из этих проблем - очень низкие амплитуды двух низших мультиполей (сферических гармоник) реликтового фона: квадруполя и октуполя. Эта проблема была известна и ранее, то только в очень точных данных WMAP она встала "во весь рост". На самом деле самой низкой сферической гармоникой является диполь. Он описывает поведение реликта на угловых масштабах равных 180o : в одном полушарии небесной сферы температура и яркость микроволнового фона оказывается выше, а в другой - ниже. К сожалению эту гармонику невозможно отделить от влияния на фон эффекта Допплера, связанного с движением наблюдателя. Вторая гармоника (квадруполь) описывает распределение флуктуаций температуры реликта на угловых масштабах в 90o, а третья гармоника (октуполь), соответственно на 60o (см. Рис. 1). Оказалось, что наблюдаемая амплитуда квадруполя составляет только 1/7 от предсказываемого теорией уровня, а амплитуда октуполя - 72% (см. Рис. 2). Это отклонение слишком велико и его трудно объяснить случайными флуктуациями наблюдаемого микроволнового космического фона. Некоторые исследователи начали предлагать ввести для объяснения этого отклонения "новую физику" (см., например, препринт astro-ph/0306597), другие с ними не соглашались. Пока, однако, никто не предложил какой-либо физический механизм, который привел бы к уменьшению амплитуд двух низших гармоник.
 |
| Рис. 1. Карта анизотропии реликтового излучения по данным WMAP (вверху), ее квадруполь (в середине) и октуполь (внизу) из препринта astro-ph/0307282. |
 |
| Рис. 2. Спектр мощности угловых распределений флуктуаций реликтового фонового излучения по данным WMAP и некоторых других экспериментов. По вертикали отложена амплитуда флуктуаций, по горизонтали номера гармоник (начиная с l=2) или угловые масштабы. Черные точки - наблюдательные данные, красная линия - предсказания теоретической модели для плоской Вселенной, лучше всего согласующиеся с наблюдениями, серая полоса - допустимая ошибка теоретических предсказаний. Слишком низкие значения двух низших гармоник показаны зеленым цветом. Низкая амплитуда только одного октуполя (l=3) недостаточно значима, но вместе с очень низкимзначением второй гармоники они становятся важным наблюдательным фактом. |
Топология
В работе, Люмине и др. опубликованной в Nature, такое решение предложено, только оно оказалось связанным не с физикой, а с геометрией, точнее с топологией.
Основная суть этого решения заключается в том, что наша Вселенная имеет конечный объем и размеры, которые не может превышать длина волны самого крупномасштабного возмущения в таком Мире. А тот факт, что мы не видим каких-либо его границ, объясняется сложной топологией. Идея Вселенной со сложной топологией отнюдь не нова. Фридмановские модели обладают самыми простыми из возможных топологий: плоская и открытая модели по топологической структуре эквивалентны плоскости, а замкнутая модель - сфере (приведены двумерные аналогии). Следующая по сложности, после плоскости и сферы, фигура - тор. Только не надо его представлять в виде бублика, гораздо более подходящее для наших целей представление - прямоугольник у которого склеены противоположные стороны. Очень хорошая аналогия - экран некоторых игровых приставок: объект, уходящий за правую границу экрана, появляется слева, а ушедший вниз - сверху. При этом геометрия такого тора остается Евклидовой, т.е. параллельные линии не пересекаются, сумма углов треугольника равна 180o и т.д.
 |
| Рис. 3. Двумерный тор. |
Чтобы получить трехмерный тор надо попарно склеить противоположные стороны прямоугольного параллелепипеда (бруска). В этом случае получится бесконечное пространство не имеющее границ, но с конечным объемом, и в какую бы стороны мы ни смотрели мы будем глядеть в затылок своим собственным изображениям.
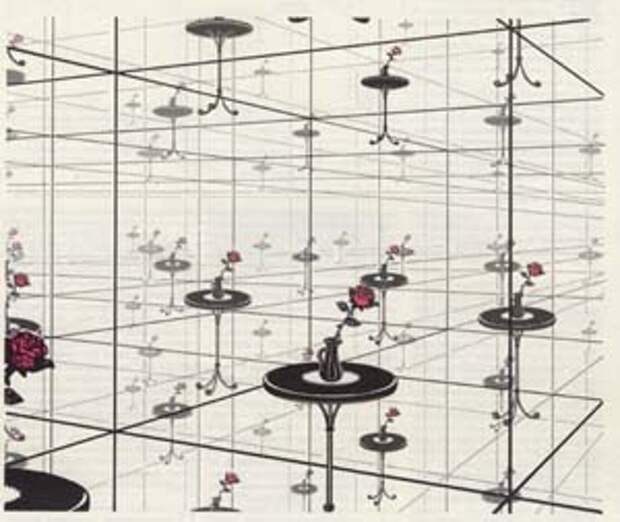 |
| Рис. 4. Вид, открывающийся наблюдателю внутри трехмерного тора, похож на то, что можно увидеть в комнате, все стены, пол и потолок которой зеркальны; только изображение, в отличие от обычного зеркального отражения, не перевернуто. Луч зрения уходит, скажем, сквозь правую стену и возвращается из левой стены; поэтому, глядя направо, наблюдатель видит комнату так, как будто он смотрит на нее снаружи сквозь прозрачную левую стену (только при этом он видит в комнате своего двойника). Аналогичные картины возникают при взгляде вперед или вверх. Так как луч зрения при продолжении неограниченно пронизывает трехмерный тор, комната будет выглядеть как простирающаяся во все стороны бесконечная прямоугольная решетка. Но трехмерный тор не бесконечен, поскольку все видимые образы, составляющие бесконечную прямоугольную пространственную решетку, - изображения одного и того же предмета. |
Давайте посмотрим из каких фигур можно строить топологически сложные пространства. Условия, которые на них налагаются логичны и понятны.
- Тела свободно пересекают грани исходной фигуры (грань - не стенка): не должно оставаться не склеенных граней.
- В пространстве нет дыр и разрывов: грани склеиваются целиком, т.е. имеют одинаковую форму.
- Тела при пересечении грани фигуры не меняют своих размеров: склеиваемые грани должны быть одного размера (они склеиваются без растяжения).
- Тела при пересечении ребра или вершины не разрываются:
- соседние грани фигуры склеиваются с соответствующей парой соседних граней;
- сумма двугранных углов вокруг ребра должна составлять 2π, а трехгранных углов у вершины - 4π.
Построение пространства со сложной топологией можно представить себе и по другому: не как склейку граней одной фигуры, а как заполнение пространства бесконечным числом копий начальной фигуры. (Перечисленные выше ограничения для такой процедуры означают, что пространство заполняется копиями фигуры без зазоров и растяжений.) Процедура заполнения пространства имеет наглядную аналогию в двумерии - задачу о "паркете" (или "мозаике") - о мощении плоскости без зазоров одинаковыми геометрическими фигурами. Плоскость можно без зазоров покрыть треугольниками, параллелограммами и центрально-симметричными шестиугольниками.
 |
| Рис. 5. Три возможных варианта покрытия плоскости правильными многоугольниками. |
Для заполнения трехмерного пространства пригодно также небольшое число фигур: параллелепипеды и шестигранные призмы. Из пяти правильных многогранников (так называемых Платоновых тел) для заполнения Евклидова пространства годится только куб (см. Рис. 6). Если для заполнения пространства используются фигуры (прямоугольные параллелепипеды, кубы, правильные шестигранные призмы) обладающие дополнительными симметриями, то соседние фигуры могут быть повернуты друг относительно друга (на 90o, 180o или 60o), что соответствует склейке граней фигуры с соответствующим поворотом. Разные "повороты" при склейке создают пространства с разными топологиями.
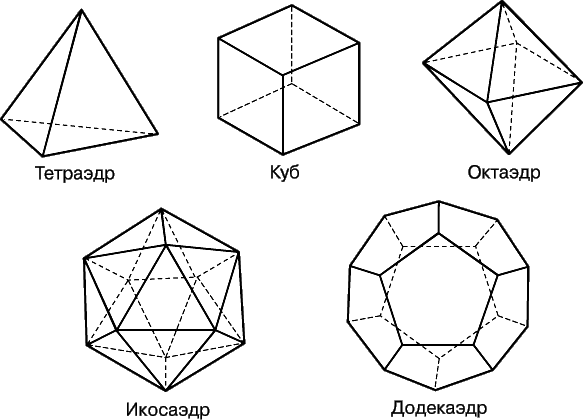 |
| Рис. 6. Правильные многогранники - Платоновы тела. Грани этих фигур являются одинаковыми правильными многоугольниками и в каждой вершине сходится одно и то же число граней. |
Искривленные пространства
А вот заполнить плоскость другими правильными многоугольниками не удастся. Например у правильного пятиугольника угол при вершине равен 108o. Если сложить три пятиугольника, то останется зазор в 36o, а если четыре, то они станут накладываться друг на друга (сумма углов при вершинах будет равна 432o, что превышает 360o). Для многоугольников с числом сторон большим шести наложение возникает уже при попытке сложить вместе три фигуры (поскольку углы правильного n-угольника равны 180o-360o/n).
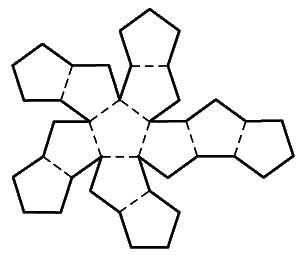 |
| Рис. 7. Попытка покрыть плоскость правильными пятиугольниками. |
Эта картина очень похожа на то, что получается при заполнении пространства додекаэдрами. Это правильные многогранники, у которых 12 граней, 20 вершин и 30 ребер, все их грани являются правильными пятиугольниками, а в каждой вершине сходятся три грани и, соответственно, три ребра (см. Рис. 6). Как при попытке сложить ребрами три таких фигуры, так и при совмещении вершин четырех многогранников остаются "щели".
Что изменится если попробовать выложить паркет не на плоской, а на кривой поверхности? Для того чтобы элементы паркета в разных местах поверхности оставались одинаковыми по форме поверхность должна обладать постоянной кривизной. В двумерном случае постоянной отрицательной кривизной обладают гиперболические поверхности, положительной - сферы, а плоскость является промежуточным случаем - поверхностью с постоянной нулевой кривизной. Примеры этих поверхностей показаны на Рис. 8.
 |
| Рис. 8. Двухмерные аналоги евклидовой, сферической и гиперболической геометрий. В плоском евклидовом пространстве параллельные прямые нигде не пересекаются, а сумма углов любого треугольника равна 180o. На сферической поверхности все параллельные пересекают друг друга, а сумма углов треугольников всегда больше 180o. На гиперболоиде сумма углов треугольника меньше 180o, а параллельные прямые расходятся. |
Прямыми на этих поверхностях являются кратчайшие линии, соединяющие пары точек. На сфере такими линиями являются дуги больших кругов (кругов, плоскости которых проходят через центр сферы). Соответственно, фигуры бывшие на плоскости треугольниками, квадратами и многоугольниками на сфере превращаются в сферические треугольники и многоугольники. Интересной особенностью этих фигур является зависимость суммы углов при их вершинах от размера фигуры (точнее от ее площади). Так у маленького сферического треугольника сумма углов только слегка превышает 180o, а у треугольника занимающего почти половину сферы она приближается к 360o(см. Рис. 9). На гиперболоиде наблюдается противоположная картина: сумма углов многоугольника меньше, чем на плоскости и убывает с ростом его размеров.
 |
| Рис. 9. С увеличением размеров сферического треугольника его углы становятся более тупыми, а их сумма увеличивается. |
Если взять правильный пятиугольник на сфере, то при определенных размерах его углы станут равными 120o (а не 108o, как на плоскости) и три таких пятиугольника будут без зазоров стыковаться друг с другом, если их сложить вершинами. Более того, двенадцать пятиугольников такого размера без зазоров покрывают всю сферу. Эта фигура вам наверняка хорошо известна: некоторое время назад так шили футбольные мячи. (Сейчас их чаще всего собирают из двух типов фигур: пяти и шестиугольников.) По-другому, показанную фигуру можно представить, как проекцию ребер и граней правильного додекаэдра на описанную вокруг него сферу.
 |  |
| Рис. 10. Футбольный мяч - сфера, собранная из двенадцати сферических пятиугольников. | |
Аналогичная картина получается при заполнении трехмерного пространства "трехмерными пятиугольниками" - додекаэдрами. Заполнить ими Евклидово пространство "без щелей" не удается. Но в пространстве положительной кривизны их углы (и двугранные углы при ребрах фигуры, и телесные при вершинах) с увеличением размеров фигуры растут таким образом, что в определенный момент все зазоры исчезают и 120 сферических додекаэдров (каждый из которых сам напоминает футбольный мяч) целиком заполняют поверхность трехмерной гиперсферы.
 |
| Рис. 11. Сто двадцать сферических додекаэдров, полностью заполняющих трехмерную гиперсферу. |
Вселенная, построенная из двенадцатигранников, обладает по крайней мере двумя преимуществами по сравнению с основанной на кубических торах.
- Додекаэдральная структура жесткая, в отличие от кубической, обладающей шестью степенями свободы (растяжения по каждой из трех осей и перекосы).
- Додекаэдральное пространство глобально однородно, его геометрия и наблюдаемый в нем спектр флуктуаций не зависят от положения наблюдателя внутри исходного многогранника.
Периодичность
Во вселенной (специально пишу это слово с маленькой буквы) конечного размера мы не можем создать структуру, масштаб которой превосходят ее размер. Склейка граней исходной фигуры или заполнение трехмерного пространства копиями исходной области приведут к тому, что в видимой нами безграничной Вселенной размеры структур и возмущений будут ограничены тем же масштабом.
А какие возмущения мы увидим на небе? Как они будут распределяться по небесной сфере во Вселенной со сложной топологией?
Если бы Вселенная не эволюционировала со временем, то все видимые нам копии исходного мира полностью совпадали бы друг с другом. Тогда во Вселенной построенной из кубов мы бы видели картину, показанную наРис. 4. Каждый объект был бы окружен шестью своими копиями, расположенными вдоль ребер куба. Дипольная и квадрупольная составляющая в такой структуре точно равны нулю, а третья гармоника (октуполь) может иметь произвольное высокую амплитуду.
Во Вселенной, построенной из додекаэдров (см. Рис. 11), картина была бы несколько другой: каждый объект был бы окружен дюжиной своих копий, в такой структуре строго равна нулю амплитуда диполя, следующие две гармоники (квадруполь и октуполь) подавлены, а амплитуды остальных определяются распределением структур в начальном многограннике. Не правда ли, эта картина очень похожа на наблюдаемую? (см. Рис. 2.)
Очень легко представить и противоположную ситуацию, когда размеры видимой части Вселенной меньше начальной фигуры. В этом случае наблюдаемая нами картина не будет отличаться от того, что мы бы увидели в бесконечной Вселенной с простой топологией (это отличие может появиться на более поздних - в космологических масштабах - временах).
На самом деле все более сложно. Когда мы наблюдаем другие галактики, то мы смотрим не только в даль, но и в прошлое. Это связано с конечность скорости света. Если бы размер нашей Вселенной составлял несколько мегапарсек, свет от копий нашей Галактики доходил бы к нам за несколько миллионов лет, за это время галактика изменяется не слишком сильно, и мы смогли бы "узнать себя" в этих "отражения", а может быть даже попытались отыскать в них Солнечную систему. Если увеличить размеры начального мира до сотен тысяч световых лет подобное опознание становится затруднительным, а узнать Млечный Путь за 2-3 миллиарда лет до нашей эры мы бы просто не смогли. Однако, все поиски периодической структуры с размерами от 1000 мегапарсек и меньше, которые проводились последние 10-20 лет, не дали положительного результата. Это означает, что если наша Вселенная и имеет ограниченный объем, то его размеры очень велики, если мы и видим самих себя, то в настолько далеком прошлом, что какое-либо отождествление с современными объектами становится практически невозможным.
Космология
Какие предсказания дает додекаэдральная модель Вселенной и как они соотносятся с наблюдениями?
В данной модели пространство должно обладать положительной кривизной (быть замкнутым), причем обладать строго определенным значением отношения средней плотности к критической Ω≃1.013 (это значение - математическая константа, которую можно вычислить с любым числом знаков после запятой). И это значение попадает внутрь допустимого диапазона! Данные WMAP дают Ω=1.02±0.02.
[Более того, если рассчитать ожидаемый спектр возмущений не для плоской модели с Ω=1, как показано на Рис. 2, а для Ω=1.013, то окажется, что и октуполь, и диполь гораздо лучше согласуются с наблюдениями!]
Как устроена такая Вселенная?
Для космологической модели с Ω=1.013 радиус горизонта будет составлять 38% от радиуса кривизны Вселенной (R), а границы додекаэдра будут лежать в интервале от 31% R (центры граней) до 39%R (вершины) от его центра. Объем такого многогранника будет составлять 83% от объема сферы горизонта. Отношение размеров додекаэдра к радиусу кривизны остается постоянным, поскольку при расширении Вселенной эти величины изменяются пропорционально друг другу. Горизонт Вселенной ведет себя по-другому. Его поведение зависит от закона расширения, более подробно это описано в статье Будущее цивилизаций, сверхсветовое расширение и космические горизонты (и ссылках приведенных в ней).
Пятна на небе
Сложная топология нашей Вселенной будет проявляться в наблюдения только в том случае, если размеры горизонта превосходят размеры исходного многогранника и в доступную нам область Вселенной хотя бы частично попадают участки его копий. Если же исходная фигура превосходит по размерам горизонт, но наблюдаемая картина не будет отличаться от вида бесконечной Вселенной. Схематически данное утверждение показано на Рис. 12.
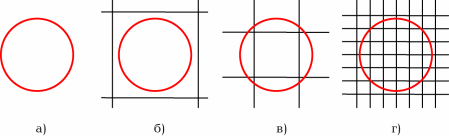 |
| Рис. 12. Возможные соотношения размеров горизонта (красная окружность) и исходных многогранников: а) бесконечная Вселенная, б) горизонт меньше исходного многогранника, в) горизонт слегка больше исходного многогранника, г) горизонт охватывает много копий исходного многогранника. В случаях а) и б) различий наблюдаться не будет. |
Для указанного выше размера горизонта (0.38R) наличие копий Вселенной будет проявляться в виде шести пар расположенных в противоположных направлениях на небесной сфере кругов диаметром 70o. Они образуются при пересечении сферы последнего рассеяния с гранями додекаэдра. Сфера последнего рассеяния (граница рекомбинации) по данным WMAP расположена на среднем красном смещении z=1089±1, т.е. слегка меньше горизонта. Температура реликтового излучения в каждом из кругов такой пары будет одинаковым образом отличаться от среднего ее значения, т.к. регистрируемое от кругов излучение испускается областями Вселенной, заполненных одним и тем же веществом (см. Рис. 13).
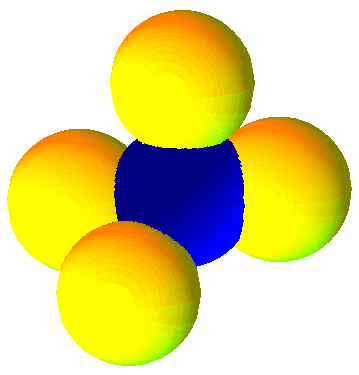 |
| Рис. 13. Пересекающиеся сферы последнего рассеяния для основного многогранника (показана синим цветом) и для некоторых его копий (желтым). |
Теоретические аспекты
То, что наша Вселенная может оказаться замкнутой, ставит определенные вопросы перед инфляционным сценарием, который сегодня успешно объясняет большинство свойств окружающей нас Вселенной. Полной ясности в этой проблеме (инфляция в замкнутой Вселенной) пока нет, но, кажется, космологи готовы к ее решению.
Заключение
Как подтвердить или опровергнуть модель, описанную в данной статье? Она предсказывает два следствия, которые допускают экспериментальную проверку, причем в ближайшее время:
- Вселенная должна быть замкнутой с Ω=1.013;
- На небе должны наблюдаться 6 пар кругов диаметром 70o (центры которых соответствуют серединам граней правильного додекаэдра) распределение возмущений реликтового излучения в которых должно попарно кореллировать друг с другом.
И, конечно, остается возможность, что для приведенных в начале данной статьи фактов найдутся совсем другие объяснения. (Этого вполне можно ожидать, так как указаний в пользу именно такой топологически сложной модели Вселенной очень мало. Пока ими являются только низкие амплитуды двух первых гармоник спектра мощности реликтового излучения. Этого достаточно, чтобы начать обсуждать данную модель, но чтобы убедить научную общественность в ее "серьезности" нужны дополнительные аргументы.)
М. Е. Прохоров ГАИШ, Москва
Источник: vokrugsveta.ru.
 |
Свежие комментарии